Particle Beam Setup

Energy can be deposited into the hydro grid by an incident ion beam or electron beam.

The particle beam kinetic energy and power can be specified to vary with time, and also by various kinetic energy (KE) distributions.

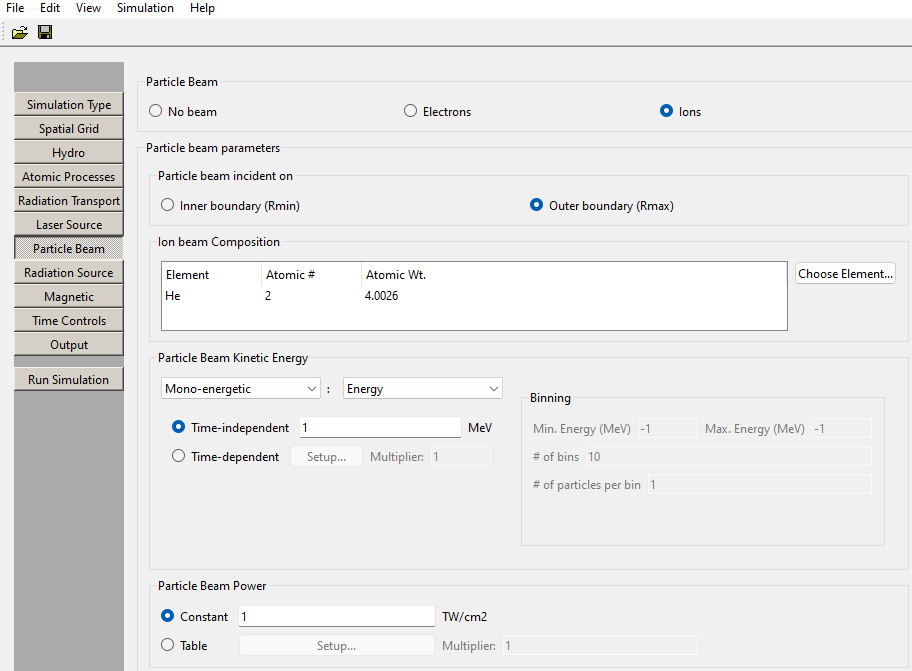
To specify the particle beam parameters:

• Select the Electrons or Ions radio button.
• Select the incident boundary for the particle beam.
• For ion beam only, specify the element by clicking on Choose Element, and selecting an element from the periodic table widget.
• Specify the kinetic energy (KE) distribution. The distribution option (e.g. Mono-energetic) appears in the first combo box. For each distribution option (except Tabulated), the distribution is defined by one or more parameters. The parameter being specified appears in the second combo box. Each parameter can be either time-independent or time-dependent.

Normalization: The distributions only define the shape. When running the simulation, Helios will normalize the distributions such that the integral of the distribution, between the Binning Min. and Max. Energy, equals the Particle Beam Power at that time. Note that the times do not need to match. Linear interpolation will be done in the case where time values do not match.

Additionally, if there are hydro times which are before the lowest input time, the value at the lowest input time will be used. Similar treatment will be done for hydro times beyond the highest input time.

Input options:

• Mono-energetic: All particles have the same kinetic energy, thus Energy is the only entry in the combo box.
• Tabulated: This option uses a multi-column table to input kinetic energy-dependent and time-dependent distributions.
  • Kinetic energies are given in the first column (which can be set using the Add Pts to X Grid button).
  • Times are specified in the top row, starting in column 2 (which can be set using the Add Pts to Y Grid button). For a KE distribution that is constant in time, only one time column is needed. If the distribution is time-dependent, additional times can be added using the Edit| | Add Column menu item, and entering its time value in the top row of the column.
  • Each remaining cell is then the dN/dE (particles per MeV) value for that energy and time. The distribution at each time is normalized to give the specified Particle Beam Power.

    An example for two times (1 and 2 nsec) is shown below. For each of the 4 beam energies (0.01, 0.1, 1, and 10 MeV), dN/dE is supplied.

  

   

• The Table File option can be used by browsing for a text file with the following format. This would enter the same values as the table above:

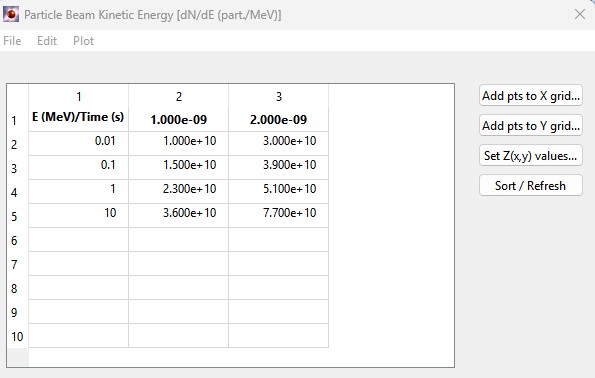
[table format=1]: Tabulated Particle beam KE:
# table rows = 4
# table cols = 3
Energy [MeV]
1.00000e-02 1.00000e-01 1.00000e+00 1.00000e+01
1e-9
1.00000e+10 1.50000e+10 2.30000e+10 3.60000e+10
2e-9
3.00000e+10 3.90000e+10 5.10000e+10 7.70000e+10

• Maxwellian: The distribution is a Maxwell-Boltzmann given by temperature T in MeV. In this case, the mean KE is also T in MeV.
• Power Law: The distribution is given by E ^-k where E is the KE, and k is dimensionless.
• Gaussian: The distribution is a Gaussian with the KE given by two parameters: the central energy E0 and standard deviation sigma. The combo box thus has an entry for both E0 and sigma.

Energy binning:

The minimum and maximum energies define the range of the distribution, and should thus be chosen to contain the significant part of the distribution . For example, E0 - 5*sigma to E0 + 5*sigma for a Gaussian, or 0.1*T to 10*T for a Maxwellian.

For Tabular input, the min. and max. should generally match the table range, unless only part of the table is desired. Outside this binning range, the beam power will be zero.

As noted above, the binning min. and max. energies also define the integration region for normalizing the energy distribution to the particle beam power.

The number of particles created per time step will be the number of bins times the number of particles per bin. It is recommended to use 25 - 100 total particles. The number of particles created with energy distributions will be a factor of (# bins x # particles per bin) more than in the mono-energetic beam.

Specify the power by either:

• Selecting Constant and entering a value or
• Selecting the Table method, clicking on Setup and entering the values of time and power for the beam. A multiplier for the power can also be entered.

Next